Uwaga
Lepsza wersja! http://jaktodziala.eu/ Rozdz. 8 Ostateczna wersja rejestru CRC
Rozdz. 8 Ostateczna wersja rejestru CRCPod rejestrem
CRC są "fotografie" 9 stanów rejestru
CRC i
Dzielna + 3 zera dla dzielnej
100011. Jest to powtórzony rys. 14.2 z
części 1 artykułu.
Zrób schemat rejestru
CRC w/g poniższego przepisu "na małpę", a układ na pewno obliczy resztę z wprowadzonej
dzielnej ( oczywiście z 3 dodatkowymi zerami) przez dzielnik
1011. Słowo harcerza.
1 - Napisz dzielnik
2 - Wstaw między bity dzielnika przerzutniki typu
D (D2, D1, D0)3 - Dokończ schemat, tak jak na rys. 15
 Rys. 15 Rejestr CRC
Rys. 15 Rejestr CRCAnalogicznie możesz zbudować
CRC dla dowolnego dzielnika. np
1011011000010101. Ważne tylko, żeby dzielnik zaczynał i kończył się
jedynką.
Pierwsze pytanie. A gdzie
ROM dzielnika? Odpowiedź- Jest ujęty w sprzężeniu zwrotnym zawierającym (lub nie)
xor-y. Super. Z układu znika
ROM.
Gdy "małpa" wystarczy - przejdź do rozdziału
9.
Gdy nie - dokończ rozdz.
8.
Najpierw o samym D Rys.15.1 Przerzutnik typu D Narastające
Rys.15.1 Przerzutnik typu D Narastające zbocze zegara (czerwone) zapamiętuje wejście
x gdzieś wewnątrz przerzutnika
. Opadające zbocze zegara (zielone) odtwarza ten stan na wyjściu
D przerzutnika. Czyli wyjście przerzutnika odtwarza stan wejścia z opóźnieniem impulsu zegarowego. Opóźnienie umożliwia realizację takich układów, jak np. rys. 15, w których na wejście mogą wchodzić sygnały zależne (tu pośrednio) od wyjścia. Możliwy jest nawet pojedynczy przerzutnik typu
D, którego wyjście (ale w stanie
następnym), zależy od tego wyjścia
D (ale w stanie
aktualnym) i od wejścia
x przerzutnika (też w stanie
aktualnym). Przykład tego znajdziesz dalej na rys. 23.
Analiza układu na rys. 15, gdy
dzielną + 3 zera jest
100011000.
Gdy wyjście D2=0 to
D1 i
D0 oraz
D0 i
komunikat będą miały bezpośrednie połączenie. Takie same jak
D2 i
D1. Dlatego że
0 XOR x =
x. Patrz rozdz. 5 cz. 1. Czyli w następnym okresie
CRC będzie zachowywał się jak zwykły rejestr przesuwny.
W stanie
0 D2=
0. Czyli następny stan
1 to przesunięte bity D1, D0 i najstarszy bit komunikatu
1, czyli
001W stanie
1 D2=
0. Czyli następny stan
2 to przesunięte bity D1, D0 i najstarszy bit komunikatu
1, czyli
010W stanie
2 D2=
0. Czyli następny stan
3 to przesunięte bity D1, D0 i najstarszy bit komunikatu
1, czyli
100 W stanie
3 D2=
1. Czyli następny stan
4 to....??? No właśnie jaki będzie ten stan
4?
Teraz: na
wejście D2 wchodzi
D0 (bezpośrednie połączenie)
na
wejście D1 wchodzi
1 XOR
D0 czyli
Negacja D0na
wejście D0 wchodzi
1 XOR
komunikat czyli
Negacja komunikatDokończmy więc przerwane wyżej zdanie.
W stanie
3 D2=
1. Czyli następny stan
4 to
011 Wyjaśnienie dla stanu 4D2=
0 bo w poprzednim stanie
3 D1=
0 a między D2 i D1 jest zwykłe połączenie
D1=
1 bo w poprzednim stanie
3 D0=
0 a na D1 wchodzi
Negacja (
D0=0), czyli
1D0=
1 bo w poprzednim stanie
3 komunikat=
0 a na D0 wchodzi
Negacja (
komunikat=0), czyli
1Jedziemy dalej:
W stanie
4 D2=
0. Czyli następny stan
5 to przesunięte bity D1, D0 i najstarszy bit komunikatu
1, czyli
111 ....
W ten sposób dojdziemy do stanu końcowego
CRC =
111 Czyli
111 jest resztą z dzielenia
100011 przez
1011Może to było mętne. W każdym bądź razie starałem się przekonać,że układ z rys. 15 oblicza resztę z dzielenia.
Rozdz. 9 Nadajnik-Odbiornik z CRC .
WstępPrzedstawione niżej rys.
17...21 zawierają wszystkie stany
Nadajnika wysyłającego do
Odbiornika komunikat
100011 wykorzystując dzielnik
1011 do wykrywania błędów. Przypomnę tylko, że dzielnik ten jest ujęty w strukturze rejestru
CRC-N nadajnika i w
CRC-O odbiornika-->
rys. 16.Rysunek ten przedstawia schemat dokładny i uproszczony. Dalej będą używane tylko schematy uproszczone
CRC (
CRC-N dla Nadajnika i
CRC-O dla Odbiornika). Gdy na torze między nadajnikiem i odbiornikiem (np w kablu) nie wystąpiły przekłamania, to
w każdym stanie wartości rejestrów CRC-N i CRC-O są takie same, co łatwo zauważyć. Stany
0...9 odpowiadają stanom
0...9 z
rys. 15. W stanie
9 w rejestrach tych będzie ta sama wartość, reszta z dzielenia
100011:1101 równa
111. Następnie w stanach
10,11,12 wartość z
CRC-N wprowadzana jest do
CRC-O, w celu ich porównania.
W stanie
12 wartość
CRC-O = 000, co oznacza, że nie wystąpiły błędy transmisji. Puste bity na rysunkach, oznaczają że nic do nich nie zostało jeszcze wpisane, albo że nie mają już żadnego znaczenia. Gdybym wpisał tam np. zera, to trudniej byłoby zauważyć, jak
"bity przesuwają się" w każdym stanie.
Rysunki
17...21 są podobne do rys.
1,2 lub
3,4. z części 1. Drobne różnice wynikają z tego, że na rys.
1,2 lub
3,4 obowiązuje reszta
zwykłego dzielenia, a na rys.
17...21 obowiązuje reszta z dzielenia
xor-owego.
 Rys.16 Rejestr CRC schemat dokładny i uproszczony
Rys.16 Rejestr CRC schemat dokładny i uproszczony Rys. 17 Nadajnik-Odbiornik stany 0,1,2Stan 0
Rys. 17 Nadajnik-Odbiornik stany 0,1,2Stan 0 Rejestr Nadajnika
RN zawiera komunikat do wysłania
+3 zera tj.
110101000. Rejestry
RN i
RO są zawsze rejestrami przesuwnymi.
W stanach
0,1,2 rejestry
CRC-N i
CRC-Ozachowują się bardzo miło. A to dlatego że jedynka nie dotarła jeszcze do najstarszego bitu. Ponieważ w najstarszym bicie jest
0, to zgodnie z algorytmem (rys. 15) w następnym stanie bity w rejestrach będą tylko przesunięte. W stanie
3 jedynka co prawda już dotarła do najstarszego bitu
CRC-N i
CRC-O. Ale dopiero w następnym stanie
4, zgodnie z algorytmem, po przesunięciu , nastąpi
xor-owanie odpowiednich bitów. Dlatego rejestry
CRC-N i
CRC-O do końca stanu
3, zachowują się jak zwykłe rejestry przesuwne. Stan wszystkich rejestrów zależy też od położeń przełączników
K1 i K2. Dotyczy to wszystkich rysunków
17...21.
stan 1 - jako następny po
stanie 0 --> rys. 15
stan 2 - jako następny po
stanie 1 --> rys. 15
stan 3 - jako następny po
stanie 2 --> rys. 15
 Rys. 18 Nadajnik-Odbiornik stany 3,4,5
Rys. 18 Nadajnik-Odbiornik stany 3,4,5Od tej pory rejestry mogą być tylko przesunięte lub przesunięte i
xor-owane . Już nie jest tak miło jak w stanach
0,1,2.
stan 3 - jako następny po
stanie 2 --> rys. 15
stan 4 - jako następny po
stanie 3 --> rys. 15
stan 5 - jako następny po
stanie 4 --> rys. 15
 Rys. 19 Nadajnik-Odbiornik stany 6,7,8stan 6
Rys. 19 Nadajnik-Odbiornik stany 6,7,8stan 6 - jako następny po
stanie 5 --> rys. 15
Cały komunikat
100011 został już przesłany do
RO. Nie ma sensu przesyłania
000. Dlatego pod koniec tego stanu zmieni się położenie przełącznika
K1. Do końca transmisji zawartość
RO nie ulegnie zmianie. Następnie będą modyfikowane tylko
CRC-N i
CRC-O. Będą też "znikać" zera w
RN.
stan 7 - jako następny po
stanie 6 --> rys. 15 (widać zmienione
K1)
stan 8 - jako następny po
stanie 7 --> rys. 15
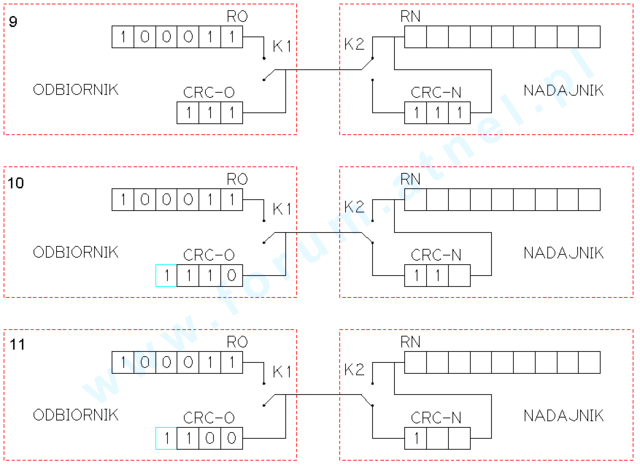 Rys. 20 Nadajnik-Odbiornik stany 9,10,11 stan 9
Rys. 20 Nadajnik-Odbiornik stany 9,10,11 stan 9.. - jako następny po
stanie 8 --> rys. 15
W
CRC-N i
CRC-O jest już ostatecznie obliczona ta sama reszta z dzielenia
111.
Ta sama-tzn. że na kablu
Nadajnik-
Odbiornik nie było zakłóceń. W następnych stanach
10,11,12 Odbiornik będzie sprawdzał, czy rzeczywiście są takie same. Dane z
CRC-N w
Nadajniku będą więc wprowadzane do
CRC-O w
Odbiorniku i porównywane
bit po bicie.Pod koniec stanu
9 zmieni się położenie
K2. W następnych stanach
10,11,12 najstarszy bit
CRC-N będzie wprowadzany do najmłodszego bitu
CRC-Ostan 10 - jako następny po
stanie 9 Widać zmienione położenie
K2. Pojawił się też dodatkowy niebieski bit, do którego będzie wprowadzany najstarszy bit z
CRC-O. Jednocześnie do najmłodszego bitu
CRC-O będzie wprowadzony najstarszy bit z
CRC-N i
natychmiast porównany z bitem niebieskim. Czyli będą porównane 2 najstarsze bity z
CRC-N i
CRC-O ze stanu poprzedniego.
Porównanie czyli
xor-owanie. Ponieważ były takie same, to w najmłodszym bicie
CRC-O będzie
0.
stan 11 - jako następny po
stanie 10.
Porównane będą 2 następne bity z
CRC-N i
CRC-O. Wynik (
0) wpisany będzie do najmłodszego bitu
CRC-O.
 Rys. 21 Nadajnik-Odbiornik stany 12 - ostatnistan 12 - ostatni
Rys. 21 Nadajnik-Odbiornik stany 12 - ostatnistan 12 - ostatni - jako następny po
stanie 11 Porównane będą 2 następne bity z
CRC-N i
CRC-O. Wynik (
0) wpisany będzie do najmłodszego bitu
CRC-O.
KONIEC!!!--ZWYCIĘSTWO. Rejestr
CRC-O =
000 oznacza, że
(z pewnym prawdopodobieństwem!) nie było błędów transmisji. Dlaczego
z pewnym prawdopodobieństwem? Mogło tak się zdarzyć, że były zakłócenia na linii, ale przypadkowo "zakłócona" liczba (inna niż nadana!) dała taką samą resztę resztę jak liczba nadana.
Podsumowanie:Każdorazowemu wprowadzeniu bitu z
RN do
RO towarzyszą aktualizacje rejestrów
CRC-N w nadajniku i
CRC-O w odbiorniku. Jeżeli na kablu
Nadajnik-Odbiornik nie było zakłóceń, to w każdej chwili
CRC-N =
CRC-O . Gdy cały komunikat znajdzie się w
RO to
CRC-N =
CRC-O =
111. W 3 następnych krokach porównujemy zawartości tych rejestrów. Końcowy stan
CRC-O = 000 oznacza, że nie było błędów.
Można zaproponować pewna modyfikację wyżej opisanej metodyWróć na chwilę do rys.
14.3 w rozdz. 8. Gdybyśmy jakimś cudem w stanie
0 znali
resztę = 111 i wstawili ją jako
111 , zamiast
000, to w stanie
9 będzie
CRC = 000. Można teraz zaproponować 2 wersje zmodyfikowanej metody.
Metoda nr 1 Prymitywna. Są 2 cykle. W pierwszym cyklu obliczymy resztę
111. Drugi cykl, to powtórzony pierwszy tylko zamiast
000 damy resztę
111. Obliczona w 2 cyklu reszta =
000, oznacza że nie było błędów. Podstawowa wada, to 2 razy wydłużony czas transmisji.
Metoda nr 2 Zauważmy, że
CRC w stanach 0...6 na rys.
14.2 i 14.3 nie różnią się. Jest to oczywiste, bo 3 ostatnie bity
000 lub
111 jeszcze nie dotarły do
CRC. Zapamiętajmy więc stan
CRC w stanie
6 w jakimś rejestrze pomocniczym. Potem w 3 krokach dojdziemy do staniu
9, w którym mamy obliczoną resztę
CRC=111. Teraz wprowadźmy z rejestru pomocniczego do
CRC ten zapamiętany stan
6 (
CRC=100). Czyli sztucznie wróciliśmy do stanu
6. Zaś do rejestru
Dzielna + 3 zera wprowadzimy resztę
111 (którą już znamy!). Dojdziemy do stanu końcowego
CRC = 000. Oznacza ,że transmisja była bezbłędna! I zrobiliśmy to tylko w
jednym cyklu. Co prawda, wydłużonym o 3 dodatkowe kroki. Nie będę analizował elektroniki dla zmodyfikowanej metody a ściślej dla metody nr 2 .Chyba jest trochę bardziej skomplikowana niż na rys.
17...21 Rys. 22 Metoda zmodyfikowana Rozdz. 10 Takie sobie rozważania o dzielnej, dzielniku i rejestrze CRC
Rys. 22 Metoda zmodyfikowana Rozdz. 10 Takie sobie rozważania o dzielnej, dzielniku i rejestrze CRCCzęsto słyszymy coś takiego. Komunikat ma 10 000 bitów. Wystąpiły przekłamania tylko na 2 pozycjach bitowych tego komunikatu.
Dany algorytm ze 100% pewnością wykrywa te przekłamania. Tu powinna się zapalić czerwona lampka. Przecież nie ma rzeczy w 100 % pewnych. Nie mam przecież 100% pewności, że jutro nie zapuka do mnie Jej Wysokość Królowa Elżbieta II i powie "hello". Prawdopodobieństwo że takie zdarzenie zajdzie (tzn. jutro ta pani nie zapuka) to jest 99,99999999999...%. Ale nie 100%. Dlatego zdanie o tych 2 przekłamaniach powinno brzmieć.
Dany algorytm ze 100% pewnością wykrywa te przekłamania powstałe na torze sygnałowym między Nadajnikiem i Odbiornikiem. Czyli milcząco zakładamy, że elektronika nadajnika i odbiornika realizuje ze 100% pewnością dany algorytm. Elektronika jak żona Cezara, jest poza wszelkimi podejrzeniami.
Poważni ludzie zamiast słowa
dzielna używają
komunikat lub
wiadomość lub
message. Tak samo zamiast
dzielnik mówią
wielomian generujący lub
generator. Nie znalazłem innych nazw dla rejestru
CRC, w którym będzie wynik
reszta z dzielenia. Tu liczę na pomoc czytelników.
Dzielnik może być przedstawiony, tak jak dotychczas, tzn. jako liczba binarna np.
Dzielnik =
1011. Symbol
1011 to skrócony zapis
1x
2^
3 +
1x
2^
1 +
1x
2^
0, gdzie
3 to nr najstarszego bitu, a
0 to nr najmłodszego. Nie powinienem tego pisać na szacownym forum, ale tak tylko sobie powiem, że
2^
0 =
1. Jest też inna forma przedstawiania dzielnika. Zamiast
Dzielnik =
1011, można napisać
Wielomian generujący =
x^
3 +
x^
1 +
1. Zauważ, że dla
x=
2 wartość tego wielomianu odpowiada dokładnie
1011=9.
Porozmawiajmy teraz o samym
dzielniku ( inaczej,
wielomianie generującym lub
generatorze). Jak go dobierać, jaka powinna być jego długość ...itp. Powinien zaczynać i kończyć się na
1. Czyli może to być np.
11,
101 lub
100001. Odpada za to
001 lub
00110100. Dlaczego? Chyba dlatego, że zera z lewej i prawej strony nie zawierają informacji ważnej dla obliczania reszty z dzielenia.
Zaczniemy od najprostszego
dzielnika=
11 lub inaczej
wielomian generujący =
x^
1 +
x^
0 =
x +
1. Odpowiada mu 1-bitowy rejestr
CRC.
 Rys. 23 CRC dla dzielnika 11
Rys. 23 CRC dla dzielnika 11Rejestr
CRC został zrealizowany zgodnie z rys. 15. Nowy stan przerzutnika
D0 jest
xor-em z wejścia i poprzedniego stanu
D0. Gdy na wejściu jest
0 to stan się nie zmieni (jak było
0 to będzie
0, jak
1 to też
1). Gdy na wejściu jest
1, to stan zmieni się na przeciwny. W technice cyfrowej
toto nazywa się
dwójka licząca lub
przerzutnik typu T. Analizę pozostawiam Czytelnikowi.
To jest klasyczny układ z bitem parzystości! Rzeczywiście, zakładając że stanem początkowym jest
D0=0, to jeżeli nie było przekłamań to bit ten pozostanie też
0. Gdy nie ma błędów, to
(jednobitowe!) rejestry
CRC-N i
CRC-0, są zawsze takie same. Niestety, tu nie mamy pewności, że błędy nie wystąpiły. Po każdej parzystej liczbie błędów rejestry
CRC-N i
CRC-O też będą takie same. Czasami jednak korzystamy z takich układów. Np. gdy komunikaty są krótkie, lub wiemy z doświadczenia że układ jest pewny i rzadko występują przekłamania. Jeżeli już, to bardzo rzadko pojedyncze przekłamanie, a podwójne to "prawie nigdy".
 Rys. 24 Przerywnik żartobliwy trochę - Inna realizacji dzielnika 11
Rys. 24 Przerywnik żartobliwy trochę - Inna realizacji dzielnika 11Żeby było jasne. Na górze widzisz paluszki projektanta. Tak wyglądał przerzutnik lampowy komputera z 1958 r. Taki mały, a przechowuje
cały jeden bit. Z wikipedii.
Dlaczego CRC mimo wszystko przepuszcza błędy? Odpowiedź jest prosta. Przecież
CRC oblicza resztę z dzielenia
komunikatu przez
wielomian generacyjny. Do znudzenia wałkowaliśmy przykład obliczania
reszty z dzielenia liczby
100011 przez
1011. Pamiętamy że reszta to
111. Jest to co prawda reszta z dzielenia
xor-owego, ale jest pełna analogia do dzielenia zwykłego. Np
327 :
13 =
25 reszta
2. Zauważ, że taką samą resztę otrzymamy gdy wykonamy
314 :
13 =
24 reszta
2, lub
301 :
13 =
23 reszta
2 itd. Gdyby więc na kablu
Nadajnik -
Odbiornik jakiś złośliwy chochlik podmienił wysyłane z
Nadajnika 327 na
314 lub
301 , to w
CRC-N nadajnika i w
CRC-O odbiornika byłyby takie same reszty
2. A ponieważ w
CRC-O występuje odjęcie tych wartości (patrz stany
10...12 w rozdz.
10), to nadajnik na podstawie
CRC-O = 000, wyciągnie fałszywy wniosek, że nie było błędów.
Jaki powinien być dzielnik, żeby przepuszczał najmniej błędów?Odpowiedź jest trudna. Z tego robi się doktoraty lub prace habilitacyjne. Tu pytanie do znawców tematu. Czy w ogóle ma ono sens?
Jaki wielomian generujący o danej ilości bajtów-1,2,3 lub 4, zapewnia najmniejszą liczbę błędów transmisj?. Byłem prawie pewien, że dla współczesnej matematyki to sprawa zamknięta. Jak twierdzenie Pitagorasa. Z internetu odniosłem jednak wrażenie, że temat stale się rozwija. Trafiłem na dyskusję z 2006 r gdzie bardzo poważni panowie, kłócili się czy ten wielomian jest lepszy czy inny. Z niecierpliwością czekam na jakiś komentarz, np biegłego magistranta. To teraz jako maluczki powiem to co wiem o
dzielniku, albo się domyślam.
1- Powinien zaczynać i kończyć się
jedynką - była o tym mowa wczęśniej
2- Im większy dzielnik tym mniej przepuszcza błędów. Wcześniej stwierdziliśmy, że dla np
327 :
13 resztą jest
2. Ta sama reszta
2 będzie też dla dzielnej
314,
301 i innych. Wystarczy więc zwiększyć ...
dzielnik np na
47, żeby dzielnych, które dają tę samą resztę (tu dla
327 :
47 =
6 reszta
45),
było mniej.
...
Wniosek - Większy dzielnik-->mniej błędów. W przypadku dzielenia
xor-owego jest jeszcze prościej. Więcej bitów ma dzielnik-->mniej błędów. To jest chyba pewne.
3 - Chociaż komunikat wysyłany jest
bit po bicie, to wiadomo że bity te zorganizowane w bajty. Dlatego dzielnik też będzie miał strukturę bajtową + 1 bit najstarszy. Dzięki temu nasz rejestr
CRC będzie miał pełne bajty. W praktyce 1,2 3 lub 4.
4- To teraz pytanie na deser. Jaki
dzielnik "4-bajtowy + 1 bit" (inaczej
wielomian generujący lub
generator) przepuszcza najmniej
dzielnych (komunikatów) które dają tę samą resztę. Inaczej - przepuszcza najmniej błędów.
Odpowiedź jest banalnie prosta. Jest to liczba
1.0000.0100.1010.0001.0001.1101.1011.0111. Dlaczego? Chyba każdy to widzi.
Oczywiście to żart!. Ale zastanawiam się jak ludzie do tego doszli? Przecież tu jest chyba ponad 4 miliardy kombinacji. Czy poprzez twierdzenia algebry wyższej? A może symulacje. Sprawdzamy wszystkie możliwe 33 bitowe kombinacje, przy wszystkich kombinacjach komunikatów o długości np. 1024 bajty. Może wystarczą krótsze np. 128 bajtów? I wybierzemy taką, która daje najmniej reszt. Może to jest właśnie ta w/w liczba? Może ktoś rozwinie ten temat? Tak przy okazji. Używasz tego
dzielnika codziennie jako wielomian używany w standarcie ETHERNET tzw CRC-32.
Postać wielomianowa dzielnika
CRC-32 = x^32 + x^26 +x^22 + x^16 + x^12 + x^11 + x^10 + x^8 +x^7 ++ x^5+ x^4 + x^2 + x + 1. Aby zbudować rejestr
CRC dla tego wielomianu wystarczy oczywiście skorzystać z rys. 15. Tu już nie żartuję.
Podam jeszcze 2 często używane wielomiany generujące
Wielomian używany przez protokoł HDLC
CRC-16 = x^16 + x^15 + x^2 + 1Standart CCITT CRC-CCITT = x^16 + x^12 + x^5 + 1Nie jestem tego pewien, ale
CRC na rys. 23 to realizacja wielomianu
CRC-2 = x+1 . Mądrych ludzi proszę o potwierdzenie. Jeżeli takowego nie ma, to zdanie to traktuj z przymrużeniem oka!
NAJWAŻNIEJSZE - JAKA JEST SKUTECZNOŚĆ WYKRYWANIA BŁĘDÓW!!!!Znalazłem coś takiego dla
CRC-16Metodą CRC-16 można wykryć :
- wszystkie
pojedyncze błędy transmisji (błędy tylko w jednym bicie) -
komentarz - Nic wielkiego,to robi głupi przerzutnik na rys. 23!
- wszystkie
podwójne błędy -
komentarz - Nie rzuca na kolana, ale może być
- wszystkie błędy
w nieparzystej ilości bitów
- wszystkie błędy w bloku do 16 bitów
-
99,9984% pozostałych błędów transmisji.
I to jest samo miodzio - bardzo ważna informacja. Nie wiem czy mam rację, ale podejrzewam że 0,0016% błędów wiąże się "z tymi samymi resztami" omówionymi wcześniej.
Nie znalazłem danych dotyczących
CRC-32. Podejrzewam, że jako metoda używająca 2 razy większego
dzielnika będzie dużo lepsza od
CRC-16.
Jeszcze taki mały paradoks. Zauważ że
CRC-16 wykrywa w 100% błędy transmisji, które "tylko trochę" zniekształcają informację wyjściową np. w 1 bicie lub kilku. Jest to oczywiste. Przypominam że w
CRC siedzi reszta z dzielenia
komunikatu (liczby którą Nadajnik wysyła do Odbiornika) przez jakiś
dzielnik. Nie jest to zwykłe dzielenie, ale
xor-owe. Nie mniej jednak efekty tych
dzieleń (
"zwykłych" i
xor-owych) są podobne. Wiadomo że np. reszta z dzielenia np.
578:19 to
8. (578=19x30 +
8). Zauważ jednak że ta sama reszta =
8, będzie też przy wysyłanym komunikacie
559,
540,
521...
46,
27 i
8. Czyli gdyby komunikat został "zniekształcony" do w/w liczb to byłaby ta sama reszta
8 i Odbiornik potraktujemy odebrany komunikat jako bezbłędny. To gdzie ten paradoks? No właśnie. Gdy zniekształcenie jest małe, np Odbiornik odebrał liczbę
576 (zamiast
578, to na 100% błąd ten będzie wykryty, bo na 100% będzie inna reszta. Gdy zniekształcenie jest duże (w krańcowym wypadku zupełnie przypadkowa liczba) to odbiornik wykryje ten błąd, ale z prawdopodobieństwem np.
99,99%, a nie
100%. To
0,01% to wtedy, gdy przypadkowo reszta będzie taka sama, chociaż komunikat będzie zupełnie inny.
Gdyby te reguła obowiązywał w życiu codziennym, to na 100% odróżnimy strongmana Pudzianowskiego od jego podobnego brata bliźniaka (gdyby miał takowego), ale tylko na 99,99% od jakiegoś przedszkolaka.
Rozdz. 11 Prawdziwy Nadajnik-Odbiornik z CRCRys. 25 jest uogólnieniem
rys.17...21 z
rozdz. 10Różnice są następujące
Rys. 17...21 - 1 komórka oznacza
1 bitRys. 25 - 1 komórka oznacza
1 bajt (oprócz komórki "niebieskiej" w stanach
10...12, która jest
bitem)
Rys. 17...21 -
RN dla komunikatu
6-bitowego +
3 zeraRys. 25 -
RN dla komunikatu
1020-bajtowego +
4 bajtowe zera (czyli 8160 bitów +
32 zera)
Rys. 17...21 -
RO dla komunikatu
6-bitowego Rys. 25 -
RO dla komunikatu
1020-bajtowego + (czyli 8160 bitów)
Rys. 17...21 CRC-N i
CRC-O 3-bitowe realizujące dzielnik =
1011Rys. 25 CRC-N i
CRC-O 4-bajtowe (32-bitowe) realizujące dzielnik
CRC-32 =
1.0000.0100.1010.0001.0001.1101.1011.0111Wspólnymi cechami dla rys. 17...21 i 25 są:- transmisje między rejestrami są takie same
tzn. po jednym bicie!- "niebieska"
jednobitowa komórka jako przedłużenie rejestru
CRC-O-
gdy na kablu Nadajnik-Odbiornik nie ma zakłóceń, to w każdym stanie w rejestrach CRC-N i CRC-O są takie same wartości! rys. 25 Nadajnik-Odbiornik z 4-bajtowym CRC i z 1020-bajtowym komunikatemRys. 17...21
rys. 25 Nadajnik-Odbiornik z 4-bajtowym CRC i z 1020-bajtowym komunikatemRys. 17...21 odnoszą się do sytuacji "dydaktycznej", gdzie komunikat miał tylko 6 bitów. Dlatego bez problemu można było przedstawić "fotografie" wszystkich 12 stanów.
Rys. 25 dotyczy komunikatu o długości 8160 bitów nie mówiąc już o 32 zerach. Trudno byłoby przestawić 8192 "fotografii" dla wszystkich stanów. Okazuje się, że można to zrobić na 3 "fotografiach", jak na
rys. 25. Każdej fotografii przyporządkowany jest symbol
0...6,
7...9 lub
10...12.
Stanom
0...6 na
rys. 25 odpowiadają te stany na
rys. 17...19Stanom
7...9 na
rys. 25 odpowiadają te stany na
rys. 19...20Stanom
10...12 na
rys. 25 odpowiadają te stany na
rys. 20...21Opis poszczególnych stanów na rys. 25 Uwaga - komórki to
bajty a nie
bity (oprócz "niebieskiej", która jest bitem)
Stany 0...6 - Przesuwanie komunikatu z
RN do
RO. Aktualizacje
CRC-N i CRC-O.
Stan 0 RN komórki 0...3 -
4 x zero (czyli
32 zerowe bity)
RN komórki 4...1019 -
komunikat CRC-N i CRC-O - wyzerowane
Stany 1...5W tych stanach komórki będą stopniowo wprowadzane z
RN do
RO,
CRC-N i
CRC-O. W każdym kroku będą odpowiednio modyfikowane rejestry
CRC-N i
CRC-O. Rejestr
RO będzie się "wydłużał" do lewej strony a rejestr
RN będzie się skracał z prawej strony.
Stan 6 RN - tylko 4 najstarsze komórki -
4 x zero (czyli
32 zerowe bity), pozostałe nieistotne
RO -
Komunikat zajmuje cały rejestr. Ze względu na stan przełącznika w stanach 7...12,tak będzie już do końca.
CRC-N i CRC-O - takie same wartości.
Stany 7...9 - Komunikat w
RO ustalony. Tylko aktualizacje
CRC-N i CRC-O.
W stanie
9 w
CRC-N i CRC-O są już
te same, ostatecznie obliczone wartości
reszt.
Stany 10...12 - Komunikat w
RO ustalony. Porównywanie wartości w
CRC-N i CRC-O.
"Niebieski" bit pełni dokładnie taką samą rolę w porównywaniu, jak na
rys. 20, 21 w stanach
10...12W stanie końcowymRN - "pusty" (zera albo nieistotne)
R0 - komunikat
CRC-N - "pusty" (zera albo nieistotne)
CRC-O - gdy nie było błędów -->
wyzerowany........- gdy były-->wartość
niezerowaGdy
Odbiornik na podstawie
CRC-O stwierdzi, że były błędy, to może zażądać od
Nadajnika ponownego przesłania komunikatu.
Rozdz. 12 Programowe obliczanie reszty CRC - metoda SIMPLE (1-bitowa)Do tej pory reszta była obliczana w
CRC metodą bit po bicie. Przy okazji proszę zwrócić uwagę jak prosty jest ten hardware (rys. 15). Nawet gdyby realizowany był wielomian
CRC-32. Rysunek miałby wtedy 32 przerzutniki D i inną konfigurację
xor-ów. Też byłby to w miarę prosty układ, który jednak potrafi obliczyć resztę z dzielenia np. liczby 1000 bajtowej przez 4 bajtową. I to prawie nie opóźniając transmisji. A co zrobić gdy nasz mikrokontroler nie ma wbudowanego mechanizmu
CRC? Jedyne wyjście to metody
programowe. Zaczniemy od metody
SIMPLE. Jest to bezpośrednia realizacja programowa algorytmu "rejestrowego". Jedynego jakiego znamy do tej pory. Niestety, program bardzo zmniejsza prędkość transmisji, ponieważ realizowany jest metodą "bit po bicie".
 Rys. 26 Jakie będzie CRC po wprowadzeniu 1 bitu?Rys. 26a - bit sterujący 0Lewa strona -wersja "rejestrowa" algorytmu
Rys. 26 Jakie będzie CRC po wprowadzeniu 1 bitu?Rys. 26a - bit sterujący 0Lewa strona -wersja "rejestrowa" algorytmuDzielnik 1
011011. (Najstarszy bit zawsze 1, lecz tylko "czerwone" bity wpływają na algorytm)
Aktualny stan
CRC=011001 widoczny w górnym wierszu prostokąta (1 "czeka" na wejściu)
Bit sterujący (najstarszy)
CRC=0, dlatego bity będą tylko przesunięte w lewo.
Prawa strona - wersja "xor-owania pisemnego z 2 kreskami"Czyli inna wersja algorytmu dająca ten sam wynik.
Pod dolną kreską
0110011 CRC+"czekająca" jedynka. Nazwijmy to dzielną.
Bit sterujący
CRC=0, dlatego dzielną należy
xor-ować z przesuniętymi
000000 o 1 bit w prawo. Wynik widoczny nad górną kreską. Taki sam jak w dolnym wierszu prostokąta.
Rys. 26b - bit sterujący 1Lewa strona -wersja "rejestrowa" algorytmuAktualny stan
CRC=111001 widoczny w górnym wierszu prostokąta (1 "czeka" na wejściu)
Bit sterujący (najstarszy)
CRC=1, dlatego bity będą
- przesunięte w lewo (jak w dolnym wierszu prostokąta z lewej strony) a potem
-
xor-owane z czerwonymi bitami
011011 dzielnika (jak w dolnym wierszu prostokąta "środkowego")
Prawa strona - wersja "xor-owania pisemnego z 2 kreskami"Pod dolną kreską
0110011 CRC+"czekająca" jedynka. Nazwijmy to dzielną.
Bit sterujący
CRC=1, dlatego dzielną należy
xor-ować z przesuniętymi czerwonymi bitami
011011 dzielnika. Wynik widoczny nad górną kreską. Taki sam jak w dolnym wierszu prostokąta środkowego.
Uwaga Nazwa
"sterujący" najstarszego bitu
CRC jest chyba oczywista. Gdy
0 to tylko przesunięcie. Gdy
1 to przesunięcie +
xor-owanie z "czerwonymi" bitami dzielnika.
Rys. 26c - wersja "tablicowa" algoryrmuJest odpowiednikiem "
xor-owania pisemnego z 2 kreskami"
Lewa stronaW czarnym prostokącie jest aktualny stan
CRC=111001. Z prawej strony "czekająca" jedynka
Pod rejestrem tablica z wierszami o adresach 0 i 1
- wiersz o adresie 0 zawiera
000000- wiersz o adresie 1 zawiera
011011 (czerwone jedynki dzielnika)
Środek stronyBity w czarnym prostokącie + lewa jedynka są przesunięte w lewo. Tu sterujący bit
1 (najstarszy)
CRC został "wypchnięty" w lewo. Ponieważ bit sterujący =
1, to rejestr
CRC będzie
xor-owany z wierszem o adresie też
1. Wynik tego
xor-owania będzie widoczny na prawej stronie.
Prawa stronaOstateczny wynik operacji.
CRC = 001000Uwaga. Gdyby na początku (lewa strona) było
CRC=011001 , to bitem sterującym będzie
0. Wtedy po przesunięciu
CRC będzie
xor-owane z zawartością wiersza o adresie
0. Czyli wynikiem będzie
110011.
Zarys programu obliczającego resztę CRCNiniejszy program będzie obliczał resztę tak jak na rys. 15.
Tzn. Przesyłaną wiadomością jest
100011Dzielnikiem jest
1011Program w C-podobnym języku
bunga-bunga powinien policzyć resztę z dzielenia
100011:1011Wyzeruj rejestr CRC (3 bity)
Dopisz do wiadomości 3 zera - stan 0 na rys. 15
WHILE(jeszcze nie jest wprowadzona cała wiadomość z zerami){...
PRZESUŃ CRC o jeden bit w lewo i wprowadź najstarszy bit wiadomości z zerami do CRC...
IF(wychodzący bit jest 1) (XOR-uj CRC z 011)}Przetestuj ten program pomagając sobie rys.15, a przekonasz się że na końcu
CRC=111Rozdz. 13 Programowe obliczanie reszty CRC - metoda tablicowa ĆWIERĆBAJTOWA (2-bitowa)Od razu zastrzegam, że metoda ta nie jest (chyba?) stosowana w praktyce. Potraktujmy ją jako wstęp dla metody " prawdziwej" tj
tablicowej "BAJTOWEJ".
Z załączonego na końcu poprzedniego programu wynika, że wysłanie jednego bitu wymaga 2 instrukcji w języku wyższego poziomu niż assembler (np.
C). Odpowiadać to może, tu strzelę np. 10 instrukcjom maszynowym. Może trochę upraszczam, ale zakładając że transmisja jednego bitu odpowiada jednej instrukcji maszynowej, to od razu rzuca sie w oczy jak program może opóźniać transmisję! Jak zwiększyć "szybkość" programu? Nie trzeba być Eugeniuszem żeby zaproponować wprowadzanie dwóch bitów (ćwierćbajtu) jednocześnie do rejestru
CRC.
Przy wprowadzaniu do CRC 1 bitu tablica zawiera tylko 2 wiersze (rys. 26c). Pierwszy o adresie 0 gdy bitem sterującym jest 0 i drugi o adresie 1, gdy bitem sterującym jest 1.
Przy wprowadzaniu do CRC 2 bitów, będą odpowiednio 4 kombinacje bitów sterujących, czyli najstarszych 2 bitów rejestru CRC - 00, 01, 10 i 11. Czyli tablica będzie 4 wierszowa. W zależności od tych bitów, rejestr będzie odpowiednio przesuwał i (ewentualnie)
xor-ował swoje bity. Rozpatrzmy więc te 4 kombinacje.
Pierwsza kombinacja - bity sterujące 00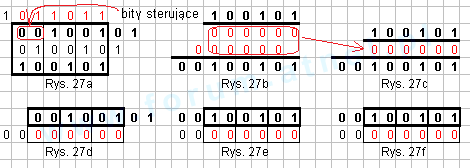 Rys. 27 Jakie będzie CRC po wprowadzeniu "ćwierćbajtu" (2 bitów)? - bity sterujące 00Rys. 27a - wersja algorytmu "rejestrowa"
Rys. 27 Jakie będzie CRC po wprowadzeniu "ćwierćbajtu" (2 bitów)? - bity sterujące 00Rys. 27a - wersja algorytmu "rejestrowa" Dzielnik 1
011011. (Najstarszy bit zawsze 1, lecz tylko "czerwone" bity wpływają na algorytm)
Aktualny stan
CRC=001001 widoczny w górnym wierszu prostokąta (
01 "czeka" na wejściu). Bit sterujący (najstarszy)
CRC=0, dlatego bity będą tylko przesunięte w lewo.Efekt
010010 widać w środkowym wierszu. Tu znowu bit sterujący
CRC=0. Bity ponownie będą tylko przesunięte w lewo. Efekt
100101 widać w dolnym wierszu.
Akurat w powyższym przykładzie 2 pierwsze bity to
00. Dlatego zmiany w
CRC to tylko 2 przesunięcia bez
xor-owania.
Rys. 27b - Wstępna wersja algorytmu "xor-owania pisemnego z 2 kreskami" Aktualny stan + 2 bity "czekające"
CRC=00100101 pod dolną kreską.
bity
000000 nad kreską odpowiadają pierwszemu przesunięciu. Następne
000000 drugiemu. Po
xor-owaniu ostatnich 6 bitów (pod dolną kreską) z 2 wierszami, nad górną kreską otrzymamy
100101 - to samo co w dolnym wierszu prostokąta z rys. 27a.
Rys. 27c - Ostateczna wersja algorytmu "xor-owania pisemnego z 2 kreskami" Bity
000000 są wynikiem sumowania 2 wierszy
000000 na rys. 27b. Czyli
100101 nad górną kreską jest
xor-em z
100101 i
000000. Wynik oczywiście taki sam jak na rys. 27a.
Rys. 27d Wersja tablicowa algorytmu dla bitów sterujących 00 - stan początkowyW czarnym prostokącie jest początkowy stan rejestru
CRC=001001 + 2 bity "czekające"
01. Z bitami sterującymi
00 związany jest wiersz o adresie też 00, zawierający
000000Rys. 27e Wersja tablicowa algorytmu dla bitów sterujących 00 - stan pośredniBity w rejestrze należy przesunąć o 2 pozycję w lewo. Następnie rejestr
xor-ujemy z wierszem tablicy o adresie 00. czyli z
000000. Wynik tego działania będzie widoczny na rys. 27f
Rys. 27f Wersja tablicowa algorytmu dla bitów sterujących 00 - stan końcowyTaki sam wynik jak na rys. 27a.
Druga kombinacja - bity sterujące 01 Rys. 28 Jakie będzie CRC po wprowadzeniu "ćwierćbajtu" (2 bitów)? - bity sterujące 01Rys. 28a - wersja algorytmu "rejestrowa"
Rys. 28 Jakie będzie CRC po wprowadzeniu "ćwierćbajtu" (2 bitów)? - bity sterujące 01Rys. 28a - wersja algorytmu "rejestrowa" Dzielnik 1
011011.
Aktualny stan
CRC=011001 widoczny w górnym wierszu prostokąta (
01 "czeka" na wejściu). Bit sterujący (najstarszy)
CRC=0, dlatego bity będą tylko przesunięte w lewo.Efekt 110010 widać w środkowym wierszu. Ale teraz bit sterujący
CRC=1. Bity ponownie będą przesunięte w lewo a potem
xor-owane przez
011011. Efekt
111110 widać w dolnym wierszu.
Rys. 28b - Wstępna wersja algorytmu "xor-owania pisemnego z 2 kreskami" Aktualny stan + 2 bity "czekające"
CRC=01100101 pod dolną kreską. Bity
000000 nad kreską odpowiadają pierwszemu przesunięciu. Następne - przesunięciu i
xor-owaniu przez
011011. Po
xor-owaniu ostatnich 6 bitów (pod dolną kreską) z 2 wierszami, nad górną kreską otrzymamy
111110 - to samo co w dolnym wierszu prostokąta z rys. 28a.
Rys. 28c - Ostateczna wersja algorytmu "xor-owania pisemnego z 2 kreskami" Bity
011011 są wynikiem
xor-owania wierszy
000000 i
011011 na rys. 28b. Czyli
111110 nad górną kreską jest
xor-em z
100101 i
011011. Wynik oczywiście taki sam jak na rys. 28a.
Rys. 28d Wersja tablicowa algorytmu dla bitów sterujących 01 - stan początkowyW czarnym prostokącie jest początkowy stan rejestru
CRC=011001 + 2 bity "czekające"
01. Z bitami sterującymi
01 związany jest wiersz o adresie też 01, zawierający
011011.
Rys. 28e Wersja tablicowa algorytmu dla bitów sterujących 01 - stan pośredniBity w rejestrze należy przesunąć o 2 pozycję w lewo. Następnie rejestr
xor-ujemy z wierszem tablicy o adresie 01. Wynik tego działania będzie widoczny na rys. 28f
Rys. 28f Wersja tablicowa algorytmu dla bitów sterujących 01 - stan końcowyTaki sam wynik jak na rys. 28a.
Trzecia kombinacja - bity sterujące 10 Rys. 29 Jakie będzie CRC po wprowadzeniu "ćwierćbajtu" (2 bitów)? - bity sterujące 10Rys. 29a - wersja algorytmu "rejestrowa"
Rys. 29 Jakie będzie CRC po wprowadzeniu "ćwierćbajtu" (2 bitów)? - bity sterujące 10Rys. 29a - wersja algorytmu "rejestrowa" Dzielnik 1
011011.
Aktualny stan
CRC=101001 widoczny w górnym wierszu prostokąta (
01 "czeka" na wejściu).Bit sterujący
CRC=1. Bity będą przesunięte w lewo, a potem
xor-owane przez
011011. Efekt 001001 widać w środkowym wierszu. Ale teraz bit sterujący (najstarszy)
CRC=0, dlatego bity będą tylko przesunięte w lewo.Efekt
010011 widać w dolnym wierszu.
Rys. 29b - Wstępna wersja algorytmu "xor-owania pisemnego z 2 kreskami" Aktualny stan + 2 bity "czekające"
CRC=01100101 pod dolną kreską. Bity
011011 nad kreską odpowiadają pierwszemu przesunięciu i
xor-owaniu przez
011011. Następne
000000 - tylko przesunięciu. Po
xor-owaniu ostatnich 6 bitów (pod dolną kreską) z 2 wierszami, nad górną kreską otrzymamy
010011 (to samo co w dolnym wierszu prostokąta z rys. 29a).
Rys. 29c - Ostateczna wersja algorytmu "xor-owania pisemnego z 2 kreskami" Bity
011011 są wynikiem
xor-owania wierszy
011011 i
0000000 na rys. 29b. Czyli
010011nad górną kreską jest
xor-em z
100101 i
110110. Wynik oczywiście taki sam jak na rys. 29a.
Rys. 29d Wersja tablicowa algorytmu dla bitów sterujących 10 - stan początkowyW czarnym prostokącie jest początkowy stan rejestru
CRC=101001 + 2 bity "czekające"
01. Z bitami sterującymi
10 związany jest wiersz o adresie też 10, zawierający
110110.
Rys. 29e Wersja tablicowa algorytmu dla bitów sterujących 10 - stan pośredniBity w rejestrze należy przesunąć o 2 pozycję w lewo. Następnie rejestr
xor-ujemy z wierszem tablicy o adresie 10. Wynik tego działania będzie widoczny na rys. 29f
Rys. 29f Wersja tablicowa algorytmu dla bitów sterujących 10 - stan końcowyTaki sam wynik jak na rys. 29a.
Czwarta kombinacja - bity sterujące 11 Rys. 30 Jakie będzie CRC po wprowadzeniu "ćwierćbajtu" (2 bitów)? - bity sterujące 11Rys. 30a - wersja algorytmu "rejestrowa"
Rys. 30 Jakie będzie CRC po wprowadzeniu "ćwierćbajtu" (2 bitów)? - bity sterujące 11Rys. 30a - wersja algorytmu "rejestrowa" Dzielnik 1
011011.
Aktualny stan
CRC=111001 widoczny w górnym wierszu prostokąta (
01 "czeka" na wejściu). Bit sterujący (najstarszy)
CRC=1, dlatego bity będą przesunięte w lewo a potem
xor-owane przez
011011. Efekt 101001 widać w środkowym wierszu. Teraz bit sterujący znowu
CRC=1. Bity ponownie będą przesunięte w lewo a potem
xor-owane przez
011011. Efekt
001000 widać w dolnym wierszu.
Rys. 30b - Wstępna wersja algorytmu "xor-owania pisemnego z 2 kreskami" Aktualny stan + 2 bity "czekające"
CRC=11100101 pod dolną kreską. Bity
011011 nad kreską odpowiadają pierwszemu przesunięciu i
xor-owaniu przez
011011. Następne - drugiemu przesunięciu i
xor-owaniu . Po
xor-owaniu ostatnich 6 bitów (pod dolną kreską) z 2 wierszami, nad górną kreską otrzymamy
001000 - to samo co w dolnym wierszu prostokąta z rys. 30a.
Rys. 30c - Ostateczna wersja algorytmu "xor-owania pisemnego z 2 kreskami" Bity
101101 są wynikiem
xor-owania 2 wierszy
011011 na rys. 30b. Czyli
001000nad górną kreską jest
xor-em z
100101 i
101101. Wynik oczywiście taki sam jak na rys. 30a.
Rys. 30d Wersja tablicowa algorytmu dla bitów sterujących 11 - stan początkowyW czarnym prostokącie jest początkowy stan rejestru
CRC=111001 + 2 bity "czekające"
01. Z bitami sterującymi
11 związany jest wiersz o adresie też 11, zawierający
101101.
Rys. 30e Wersja tablicowa algorytmu dla bitów sterujących 11 - stan pośredniBity w rejestrze należy przesunąć o 2 pozycję w lewo. Następnie rejestr
xor-ujemy z wierszem tablicy o adresie 11. Wynik tego działania będzie widoczny na rys. 30f
Rys. 30f Wersja tablicowa algorytmu dla bitów sterujących 11 - stan końcowyTaki sam wynik jak na rys. 30a.
Metoda tablicowa ćwierćbajtowaMetoda pozwala na szybkie obliczenie następnego stanu
CRC po wprowadzeniu do niego "ćwierćbajtu" (2 bitów)
 Rys. 31 Jaki będzie następny stan po wprowadzeniu "ćwierćbajtu" 01?
Rys. 31 Jaki będzie następny stan po wprowadzeniu "ćwierćbajtu" 01?Na początku w
CRC było
101001 01 czeka na wejściu. Metoda pozwoli na szybkie ("w jednym ruchu") obliczenie następnego stanu
010011. Milcząco zakładamy oczywiście, że znany jest dzielnik 1
011011. Następny rysunek pokazuje jak to zrobić.
Rysunek 32 jest "złożeniem do kupy" rysunków 27,28,29 i 30 w części dotyczącej metody tablicowej (d,e,f)
 Rys.32 Przykład metody tablicowej "ćwierćbajtowej"Rys. 32a
Rys.32 Przykład metody tablicowej "ćwierćbajtowej"Rys. 32a przedstawia stan początkowy.
CRC = 101001. Na wejściu "czeka"
01. Pod rejestrem
CRC jest tablica 4 wierszowa, która "powstała" z rysunków 27d, 28d, 29d i 30d. Adres 3 wiersza
10 jest wytłuszczony, dlatego że "ćwierćbajt" sterujący (2 najstarsze bity
CRC), też jest
10.
Rys. 32b przedstawia
CRC z bitami przesuniętymi o 2 pozycje w lewo. "Ćwierćbajt" sterujący wyjdzie na zewnątrz, a do rejestru wprowadzony będzie "czekający ćwierćbaj"
01. Teraz program będzie
xor-ował
CRC z wierszem o adresie wskazanym przez "wypchnięty" ćwierćbajt" sterujący -
10. Wynik
xor-owania na rys. 32c.
Rys. 32c - Wynik końcowy
CRC=010011Widzimy że metoda tablicowa "ćwierćbajtowa" pozwala na dwukrotne przyspieszenie obliczania następnego stanu
CRC. Nic za darmo. Kosztem jest tablica. Czyli zapotrzebowanie na pamięć. Akurat w poważniejsszych mikrokontrolerach nie jest to problemem.
Zarys programu obliczającego resztę CRCNiniejszy program będzie obliczał resztę
CRC, tak obliczając następny stan
CRC jak na rys. 32.
Założenia.
Dzielnikiem jest
1011011Z powyższego wynika że
CRC jest 6-bitowe ( bo dzielnik 7-bitowy)
Przesyłaną wiadomością dowolna liczba (więcej niż 6 bitowa oczywiście).
Program w C-podobnym języku powinien policzyć resztę z dzielenia
wiadomość:1011011Wcześniej w dyrektywach program założy tablice 4x6 (4 wiersze po 6 bitów) tak jak na rys. 32. Ten kawałek nie jest pokazany w poniższym programie.
Wyzeruj rejestr CRC (6 bitów)
Dopisz do wiadomości 000000 WHILE(jeszcze nie jest wprowadzona cała wiadomość z zerami){...
Zapamiętaj"ćwierćbajt" sterujący...
PRZESUŃ CRC o 2 bity w lewo i wprowadź 2 najstarsze bit wiadomości z zerami do CRC...
XOR-uj CRC z wierszem tablicy wskazanym przez "ćwierćbajt" sterujący }Gdy cała wiadomość z dołączonymi 6 zerami zostanie wprowadzona do CRC, to program wyjdzie z pętli
WHILE {...}.
W
CRC będzie reszta z dzielenia
wiadomość:1011011Rozdz. 14 Programowe obliczanie reszty CRC - metoda tablicowa BAJTOWA (8-bitowa)Porównanie metody ćwierćbajtowej i bajtowej rys.33 i 34 Rys.33 Metoda tablicowa ćwierćbajtowa
Rys.33 Metoda tablicowa ćwierćbajtowaKrótkie przypomnienie poprzedniego rozdziału.
1 - wprowadzany jest jeden ćwierćbajt (2 bity)
2 - dzielnik 7 bitowy (1bit + 3 ćwierćbajty)
3 - rejestr
CRC 3 ćwierćbajty (6 bitów)
4 - tablica zawiera 4 wiersze po 3 ćwierćbajty (po 6 bitów)
Rys 33a Stan początkowy rejestru
CRC - ćwierćbajt
01 z prawej strony "czeka" na wprowadzenie
Rys 33b Stan końcowy rejestru
CRC - po wprowadzeniu ćwierćbajtu
Rysunki
c, d, e przedstawiają dokładnie jak realizowana jest modyfikacja rejestru
CRC po wprowadzeniu ćwierćbajtu.
Rys. 33c Stan początkowy rejestru
CRC z tablicą - ćwierćbajt
01 z prawej strony "czeka" na wprowadzenie
Rys. 33d Stan pośredni rejestru
CRC z tablicą
- przesunięcie rejestru o 2 bity w lewo ( w tym wprowadzenie ćwierćbajtu
01 i "wypchnięcie" ćwierćbajtu sterującego
10)
- adresowanie wiersza wskazanego przez "wypchnięty" ćwierćbajt sterujący (
10)
-
xor-owanie
CRC przez adresowany wiersz
11 01 10. Wynik operacji na rys. 33e
Rys. 33e - Wynik operacji
Metoda ćwierćbajtowa nie jest raczej stosowana w praktyce. Ma tylko znaczenie dydaktyczne. Tablica jest tylko 4-wierszowa ponieważ są tylko 2 bity sterujące, Dlatego możliwa jest jeszcze dokładna analiza działania rejestru dla wszystkich 4 kombinacji bitów sterujących. Natomiast rządzą te same mechanizmy jak w metodzie bajtowej.
 Rys.34 Metoda tablicowa bajtowa
Rys.34 Metoda tablicowa bajtowaJest to już metoda stosowana w praktyce. Tu akurat realizowany jest wielomian
CRC-32 stosowany w internecie. Czyli jak czytasz ten tekst, coś tam kliknąłeś, to jakiś chochlik przy pomocy tablicy majstruje w
CRC.
W odróżnieniu od metody ćwierćbajtowej
1 - wprowadzany jest jeden bajt (8 bitów)
2 - dzielnik 33 bitowy (1bit + 4 bajty)
3 - rejestr
CRC 4 bajty (32 bity)
4 - tablica zawiera 256 wierszy po 8 bajtów (po 32 bity) (256 = FF)
Podkreślam, że na rys. 33 komórki są
bitowe, na rys.34
bajtowe. Zawartość każdego bajtu przedstawiona jest tu w kodzie hexa. Metoda tablicowa
bajtowa jest rozwinięciem metody ćwierćbajtowej z poprzedniego rozdziału. Różnice są tylko "ilościowe".
Rys 34a Stan początkowy rejestru
CRC - bajt
2D z prawej strony "czeka" na wprowadzenie. Liczba
1 04 A1 1D B7 odpowiada wielomianowi
CRC-32. Bajtem sterującym jest
21=00100001.
Rys 34b Stan końcowy rejestru
CRC - po wprowadzeniu bajtu
Rysunki
c, d, e przedstawiają dokładnie jak realizowana jest modyfikacja rejestru
CRC po wprowadzeniu bajtu
2D.
Rys. 34c Stan początkowy rejestru
CRC z tablicą - bajt
2D z prawej strony "czeka" na wprowadzenie.
Rys. 34d Stan pośredni rejestru
CRC z tablicą
- przesunięcie rejestru o bajt w lewo (w tym wprowadzenie bajtu
2D i "wypchnięcie" bajtu sterującego
21)
- adresowanie wiersza wskazanego przez "wypchnięty" bajt sterujący (
21)
-
xor-owanie
CRC przez adresowany wiersz
14 23 B6 E0. Wynik operacji na rys. 34e
Rys. 34e - Wynik operacji
Tablice dla metody bajtowej są tworzone w sposób analogiczny jak dla metody ćwierćbajtowej i właściwie na tym można byłoby zakończyć artykuł. Dla czystego sumienia pokaże jednak jak to się robi.
Bajt sterujący ma 8 bitów. Odpowiada to 256 różnym kombinacjom --> tablica będzie miała 256 wierszy 4 bajtowych. Wg tej samej zasady na rys. 33 tablica ma 4 wiersze 3 razy po ćwierć bajtu, ponieważ 2 bity sterujące dają 4 kombinacje. Oczywiście nie będę tworzył 256 4-bajtowych wierszy! Po prostu nie mam zdrowia. Dla przykładu stworzę tylko wiersz o adresie
00 i
21.
Dlatego pozostałe wiersze tablic na rysunkach 34c, 34d i 34e wypełniłem przypadkowymi liczbami!.
Kombinacja - bajt sterujący 00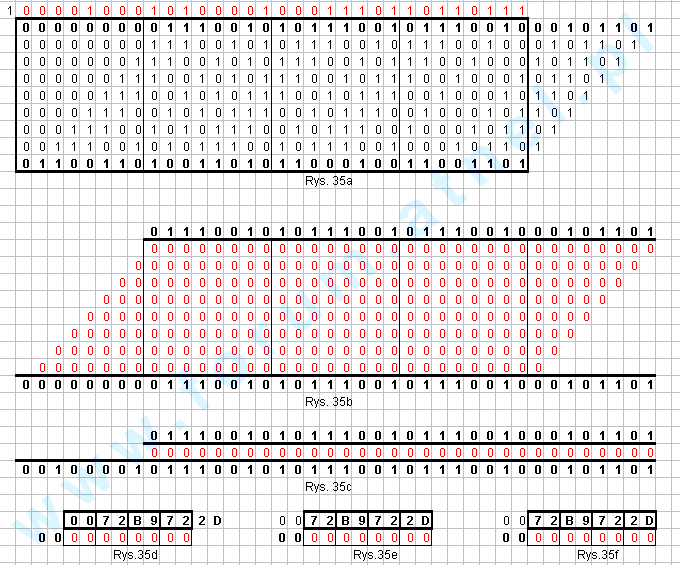 Rys. 35 Jakie będzie CRC po wprowadzeniu bajtu ? - bajt sterujący 00
Rys. 35 Jakie będzie CRC po wprowadzeniu bajtu ? - bajt sterujący 00Rys. 35 jest odpowiednikiem rys. 27. Różnice między rys. 27 i 35 są tylko ilościowe. Zasady są takie same.
Rys. 27- CRC 3 x ćwierćbajtowe (6 bitowe)
- 2 bity sterujące czyli prostokąt ma wysokość 3=2+1 wierszy (rys. 27a)
- szerokość prostokąta 3 ćwierćbajty - 6 bitów (rys. 27a)
- 2 wiersze "zerowe" między kreskami (rys. 27b)
Rys. 35- CRC 4 x bajt (32 bity)
- 8 bitów sterujących czyli prostokąt ma wysokość 9=8+1 wierszy (rys. 35a)
- szerokość prostokąta ma 4 bajty - 32 bity (rys. 35a)
- 8 wierszy "zerowych" między kreskami (35b)
Rys. 35a - wersja algorytmu "rejestrowa" Na rys. 35a, 35b i 35c dane przedstawione są w kodzie binarnym, bo liczby te łatwo się
xor-uje. W opisach natomiast przedstawione będą w kodzie hexa ze względu na ich "zwięzłość".
Dzielnik 1
04 A1 1D B7 (Najstarszy bit zawsze 1, lecz tylko "czerwone" bity wpływają na algorytm)
Aktualny stan
CRC=00 72 B9 72 widoczny w górnym wierszu prostokąta
(2D "czeka" na wejściu). Bit sterujący (najstarszy)
CRC=0, dlatego bity będą tylko przesunięte w lewo. Tu znowu bit sterujący
CRC=0 itd...Bity ponownie będą tylko przesunięte w lewo.
W ten sposób wszystkie bity będą przesunięte w lewo o 1 bajt (8 bitów) i nowy stan
CRC (9 "wytłuszczony" wiersz prostokąta) to
CRC=72 B9 72 2D.
Rys. 35b - Wstępna wersja algorytmu "xor-owania pisemnego z 2 kreskami" Aktualny stan
CRC + bajt "czekający"
00 72 B9 72 2D pod dolną kreską.
8 czerwonych zerowych wierszy nad kreską odpowiada kolejnym przesunięciom w rejestrze CRC.
Nad górną kreską (po
xor-owaniu 8 zerowych wierszy) widzimy nowy "przesunięty" stan rejestru
72 B9 72 2D. Ten sam wynik jak w dolnym wierszu na rys. 35a.
Rys. 35c - Ostateczna wersja algorytmu "xor-owania pisemnego z 2 kreskami" Bajty
00 00 00 00 są wynikiem
xor-owania 8 wierszy na rys. 35 b.Wynik oczywiście taki sam jak w dolnym wierszu na rys. 35a.
Rys. 35d Wersja tablicowa algorytmu dla bajtu sterującego 00 - stan początkowywiersz tablicy o adresie
00 wynika bezpośrednio z rys. 35c
W czarnym prostokącie jest początkowy stan rejestru
CRC=00 72 B9 72 + bajt "czekający"
2D. Z bajtem sterującymi
00 związany jest wiersz o adresie też 00, zawierający
00 00 00 00Rys. 35e Wersja tablicowa algorytmu dla bajtu sterującego 00 - stan pośredniBajty w rejestrze należy przesunąć o 1 pozycję w lewo. Następnie rejestr xor-ujemy z wierszem tablicy o adresie
00. czyli z
00 00 00 00. Wynik tego działania będzie widoczny na rys. 35f
Rys. 35f Wersja tablicowa algorytmu dla bitów sterujących 00 - stan końcowyAkurat dla tego przypadku -
xor-owanie przez zera rys. 35e i 35f są takie same.
Taki sam wynik jak na rys. 35a.
Kombinacja - bajt sterujący 21 Rys. 36 Jakie będzie CRC po wprowadzeniu bajtu ? - bajt sterujący 21Rys. 36a - wersja algorytmu "rejestrowa"
Rys. 36 Jakie będzie CRC po wprowadzeniu bajtu ? - bajt sterujący 21Rys. 36a - wersja algorytmu "rejestrowa" Aktualny stan
CRC=21 72 B9 72 widoczny w górnym wierszu prostokąta
(2D "czeka" na wejściu). Pierwszy bit sterujący (najstarszy)
CRC=0, dlatego bity będą tylko przesunięte w lewo. Tu znowu bit sterujący
CRC=0 ,czyli bity znowu będą przesunięte w lewo.
Ale teraz bit sterujący =
1. Czyli w następnym wierszu bity będą przesunięte w lewo i
xor-owane z "czerwonymi' bitami dzielnika. Tak się szczęśliwie złozyło, że przy następnych przesunięciach, bity sterujące będą
zerowe . Czyli będą tylko gołe przesunięcia, bez
xor-owań. W ten sposób po przesunięciu o bajt, dojdziemy do
wytłuszczonego wiersza nr 9 ze stanem
CRC= 66 9A C4 CB .
Uwaga Tylko jeden wiersz "do
xor-owania", to tylko przypadek! Przy innym bajcie sterującym, mogłoby być ich np. 5 a nawet 8.
Rys. 36b - Wstępna wersja algorytmu "xor-owania pisemnego z 2 kreskami" Aktualny stan
CRC + bajt "czekający"
21 72 B9 72 2D pod dolną kreską.
7 czerwonych zerowych wierszy odpowiada gołym przesunięciom w rejestrze CRC. Wiersz nr 3 - z czerwonymi bitami dzielnika, odpowiada przesunięciu i
xor--owaniu. Przy innych danych takich wierszy mogło być oczywiście więcej.
Nad górną kreską widzimy nowy stan rejestru
66 9A C4 CB. Taki sam wynik jak w dolnym wierszu na rys. 36a.
Rys. 36c - Ostateczna wersja algorytmu "xor-owania pisemnego z 2 kreskami" Bajty
14 23 B6 E0 są wynikiem
xor-owania 8 wierszy na rys. 36 b.Wynik oczywiście taki sam jak w dolnym wierszu na rys. 36a.
Rys. 36d Wersja tablicowa algorytmu dla bajtu sterującego 21 - stan początkowywiersz tablicy o adresie
21 wynika bezpośrednio z rys. 36c
W czarnym prostokącie jest początkowy stan rejestru
CRC=21 72 B9 72 + bajt "czekający"
2D. Z bajtem sterującymi
21 związany jest wiersz o adresie też
21, zawierający [img]14%2023%20B6%20E0[/img]
Rys. 36e Wersja tablicowa algorytmu dla bajtu sterującego 21 - stan pośredniBajty w rejestrze należy przesunąć o 1 pozycję w lewo. Następnie rejestr xor-ujemy z wierszem tablicy o adresie
21. czyli z
14 23 B6 E0. Wynik tego działania będzie widoczny na rys. 36f
Rys. 36f Wersja tablicowa algorytmu dla bitów sterujących 21 - stan końcowyTaki sam wynik jak na rys. 36a.
Zarys programu obliczającego resztę CRC-32Niniejszy program będzie obliczał resztę
CRC-32, tak obliczając następny stan
CRC jak na rys. 34. Jest prawie kopią programu z rozdz. 13.
Założenia.
Dzielnikiem jest 1
04 A1 1D B7Z powyższego wynika że
CRC jest 4-bajtowe (32 bo bo dzielnik 33-bitowy)
Przesyłaną wiadomością dowolna liczba (więcej niż 4 bajty oczywiście).
Program w C-podobnym języku powinien policzyć resztę z dzielenia
wiadomość:1 04 A1 1D B7Wcześniej w dyrektywach program założy tablice 256x4 bajty (256 wierszy po 4 bajty) tak jak na rys. 34. Ten kawałek nie jest pokazany w poniższym programie.
Wyzeruj rejestr CRC (4 bajty)
Dopisz do wiadomości 00 00 00 00 WHILE(jeszcze nie jest wprowadzona cała wiadomość z zerami){...
Zapamiętaj bajt sterujący...
PRZESUŃ CRC o 1 bajt w lewo i wprowadź najstarszy bajt wiadomości z zerami do CRC...
XOR-uj CRC z wierszem tablicy wskazanym przez bajt sterujący }Gdy cała wiadomość z dołączonymi 32 zerami zostanie wprowadzona do CRC, to program wyjdzie z pętli
WHILE {...}.
Wtedy w
CRC będzie reszta z dzielenia
wiadomość:1 04 A1 1D B7powrót do części 1 LINK
 Kanał - ATNEL tech-forum
Kanał - ATNEL tech-forum Wszystkie działy
Wszystkie działy Najnowsze wątki
Najnowsze wątki


















