 Uwaga
Uwaga
Lepsza wersja! http://jaktodziala.eu/Rozdz.1 - WSTĘPRozdz. 5.1.1 "Magistrala 1 Wire" - niebieska książka Mirka, dotyczy układu scalonego DS18B20. Ten wyglądający jak tranzystor maluch, potrafi zmierzyć otaczającą temperaturę, przetworzyć na wartość cyfrową np. 27,6ºC i przesłać gdzieś dalej. Już samo to jest imponujące. Ale jak się okazało, że jeszcze wykrywa błędy transmisji, to kopara już mi zupełnie opadła. Zwłaszcza, że DS18B20 wykorzystuje jakiś abstrakcyjny wielomian 8 stopnia
x^8 + x^5 + x^4 + 1. (
X^8 to
x do potęgi ósmej). Tak mnie to zaintrygowało, że zacząłem szperać w internecie. Odpuściłem sobie opracowania z dużą ilością teorii. Jakieś algebry wielomianów, ciała Galois, lematy, twierdzenia i inne bajadery. Może bym jakimś cudem przebrnął. Ale wysiłek byłby zbyt duży. Skupiłem się więc na materiałach z minimalną teorią. Tu polecałbym cykl artykułów Jarosława Dolińskiego z Elektroniki Praktycznej
http://ep.com.pl/files/4641.pdf. To co znalazłem w internecie, jeszcze bardziej okroiłem z teorii i zamieniłem w ten artykuł.
Rozdz.2 - JAK DZIAŁA WYKRYWANIE BŁĘDÓW TRANSMISJI W ŻYCIU CODZIENNYM?Błędy transmisji podświadomie wykrywamy codziennie. Pan Jourdain od Moliera też nie wiedział, że od 40 lat mówi prozą.
Przykład. Kowalski dzwoni do Nowaka i chce mu przypomnieć, że ten jest mu winien mu 32547 zł. I oczekuje od niego przelewu na tę kwotę. Jak będzie przebiegać rozmowa 2 panów?
Krok nr 1 Kowalski
mówi do Nowaka ....- Czekam na przelew 32547 zł .... Nowak notuje klnąc, że musi mendzie oddać 32547 zł.
Krok nr 2 Kowalski
powtarza ............- Czekam na przelew 32547 zł .... Nowak notuje drugi raz 32547 zł i porównuje te liczby. Jeżeli się zgadzają to oznacza, że prawidłowo odebrał informację.
Proszę zauważyć że zostały tu użyte 3 zasady wykrywania błędów transmisji.
Po pierwsze....-Kowalski i Nowak znają zasady przesyłania tej informacji. Tzn. Po nadaniu liczby "32547", należy ją jeszcze raz powtórzyć.
Po drugie.......-Informacja powtórzona nie wnosi nic nowego. Np. "żona Kowalskiego ma niebieskie oczy". Czyli jest to informacja nadmiarowa, służąca tylko do wykrywania błędów.
Po trzecie......-Sprawdzanie bezbłędności transmisji polega na tym, że Nowak porównuje informację właściwą z nadmiarową.
Rozdz.3 - KOWALSKI JAKO NADAJNIK I NOWAK JAKO ODBIORNIK Zamieńmy teraz Kowalskiego i Nowaka w elektronikę. Z rys.1 i 2 wynika że:
KOWALSKI - To nadajnik zawierający 3 elementy:RIW- pięciocyfrowy (
nie 5-bitowy!) przesuwny
Rejestr
Informacji
Właściwej. Czyli informacji do wysłania.
RIN - pięciocyfrowy przesuwny
Rejestr
Informacji
Nadmiarowej. Tu informacją nadmiarową jest po prostu powtórzona informacja właściwa.
Przełącznik - W położeniu górnym, gdy
nadawana jest informacja właściwa (rys.1) i dolnym, gdy nadmiarowa (rys.2).
NOWAK - To odbiornik zawierający też 3 elementyRO - pięciociocyfrowy przesuwny
Rejestr
Odbiorczy dla informacji właściwej.
RS - sześciocyfrowy przesuwny
Rejestr
Sprawdzający. Porównuje informację właściwą i nadmiarową. Jeżeli w transmisji nie wystąpiły błędy (czyli informacja właściwa właściwa = informacja nadmiarowa), to w stanie końcowym, 5 pierwszych cyfr będzie wyzerowanych.
Przełącznik - W położeniu górnym, gdy odbierana jest informacja właściwa (rys.1) i dolnym, gdy nadmiarowa (rys.2).
WSTĘPNY OPIS DZIAŁANIA TRANSMISJIETAP 1 Przez pierwsze 5 taktów wysyłana jest z
RIW informacja właściwa i zapisywana w
RIN,
RO i
RS-->rys1.ETAP 2 Przez następne 5 taktów wysyłana jest z
RINinformacja nadmiarowa.
-->rys.2. Teraz
RO już się nie zmienia (jest w nim cały czas odebrana informacja właściwa "32547"). Natomiast
RS przez 5 tych taktów porównuje informację właściwą z nadmiarową. Jeżeli są identyczne tzn. transmisja była bez błędów, to 5 pierwszych komórek
RS będzie wyzerowanych.
DOKŁADNY OPIS ETAPU 1 Rys.1 - Nadawanie informacji właściwej, stan początkowy, pośredni i końcowy
Rys.1 - Nadawanie informacji właściwej, stan początkowy, pośredni i końcowyPrzełączniki w pozycji
górnej.
W stanie początkowym
RIW zawiera informację do wysłania, czyli liczbę "32547". Rejestry
RIN,
RO i
RS sa wyzerowane. Każdy takt (niepokazany na rysunku impuls zegarowy) "przepycha" liczbę z
RIW do
RIN,
RO i
RS. Na rysunku pokazano stan początkowy wszystkich rejestrów, stan po 3 takcie (jako przykład stanu pośredniego) i stan końcowy nadawania informacji właściwej (po 5-tym takcie). Czytelnik sam dojdzie do wniosku, że w stan końcowy będzie następujący:
RIW = "00000",
RIN = "32547",RO = "32547" i RS = "325470" ( "0" w ostatniej "niebieskiej" komórce).
Uwaga - działanie rejestru RS!. Na rys.1 tego nie widać, ale
RS jest trochę bardziej skomplikowane od
RIN i
RO. Mianowicie, po wprowadzeniu kolejnej liczby do komórki pierwszej, natychmiast odejmowana jest od niej zawartość komórki "niebieskiej" (nr 6). Np. po trzecim takcie do komórki pierwszej wpisano "5". Natychmiast będzie od niej odjęte "0" z komórki "niebieskiej". Czyli pozostanie "5". A ponieważ w czasie nadawania informacji właściwej w komórce "niebieskiej" jest cały czas "0", to
RS zachowuje się jak zwykły rejestr przesuwny, czyli jak
RIN i
RO.
DOKŁADNY OPIS ETAPU 2 Rys.2 - Nadawanie informacji nadmiarowej, stan początkowy, pośredni i końcowy
Rys.2 - Nadawanie informacji nadmiarowej, stan początkowy, pośredni i końcowy.
Przełączniki w pozycji
dolnej.
Stan początkowy, gdy wysyłana jest informacja
nadmiarowa, rejestrów
RIW,
RIN,
RO i
RS jest taki sam, jak w stanie końcowym wysyłania informacji
właściwej (rys.1). Każdy takt "przepycha" "0" z
RIWdo
RIN,oraz liczbę z
RIN do
RS. Ze względu na stan przełącznika,
RO nie będzie zmieniane i cały czas będzie w nim informacja
właściwa - "32547". Tak, że np. po 6 takcie
RIN="03254",
RO="32547" i
RS="032547".
Uwaga! Po 6 takcie, w pierwszej komórce
RS , będzie
"0" a nie "wpychane"
"7". Przypominam, że od "wepchniętej" w 6 takcie do tej komórki "7", natychmiast odjęta będzie komórka niebieska, też "7". Czyli będzie "0". W każdym kolejnym takcie, komórka pierwsza będzie w ten właśnie sposób zerowana. Dlatego w stanie końcowym w pierwszych 5 komórkach
RS będą same zera!
Oczywiście, przy założeniu że nie było błędów transmisji!. Czyli gdy przysłana informacja nadmiarowa, też będzie równa "32547" a nie np. "39547".
Wniosek W stanie końcowym 5 zer w pierwszych 5 komórkach
RS oznacza, że w
RO znajduje się bezbłędnie odebrana informacja!
Rozdz.4 - NADAJNIK I ODBIORNIK BARDZIEJ SERIOPoprzedni rozdział dotyczył bardzo uproszczonego systemu wykrywania błędów transmisji.
Po pierwsze - Informacja właściwa była bardzo krótka, tylko 5 cyfr.
Po drugie - Informacja nadmiarowa, służąca do wykrywania błędów, była po prostu powtórzeniem informacji właściwej. Z jednej strony to bardzo dobrze. Wykryty będzie błąd na dowolnej pozycji. Czyli wykrywanie błędów będzie bardzo skuteczne. Z drugiej strony, dwukrotnie zwiększa się czas transmisji ( 2 razy wysyłane jest "32547") i zapotrzebowanie na pamięć.
Zaproponujmy więc system przedstawiony na rys.3 i 4. Też wytąpią tu 2 etapy.
Etap 1 - Wysyłanie informacji właściwej
Etap 2 - Wysyłanie informacji nadmiarowej
Z rys. 3 i 4 wynika że:
NADAJNIK zawiera 3 elementy:
Rejestr RN - 128 bajtowy rejestr nadajnika. Odpowiednik
RIW z rozdz. 3.
Rejestr CRC-N - 4 bajtowy rejestr obliczający informację nadmiarową. Odpowiednik
RIN z rozdz. 3. Na razie nie zwracajmy uwagi na tajemniczą nazwę CRC-N. "N" to oczywiście od
Nadajnika. Do nazwy CRC wrócimy później.
Przełącznik - W położeniu górnym, gdy odbierana jest informacja właściwa (rys.3) i dolnym, gdy nadmiarowa (rys.4). czyli coś znajomego.
ODBIORNIK też zawiera 3 elementy:
Rejestr R0 - 128 bajtowy rejestr odbiornika.
Rejestr CRC-O - 4 bajtowy rejestr obliczający informację nadmiarową. Niebieska komórka jest przeznaczona na dodatkowy bit (nie bajt!). Pełni podobną funkcję jak niebieska komórka w
RS w poprzednim rozdz. 3.
Przełącznik - W położeniu górnym, gdy odbierana jest informacja właściwa (rys.3) i dolnym, gdy nadmiarowa (rys.4). Czyli coś znajomego.
Działanie jest podobne do rozdz. 3. Z tym że informacją nadmiarową nie może być już powtórzona informacja właściwa. Trudno żeby w 4 bajtach CRC-N lub CRC-O zmieściła się liczba 128-bajtowa! Musimy zastosować jakąś sztuczkę. Będzie to dzielenie 128 bajtowej liczny z RN przez
"jakąś" liczbę.
Najważniejsze. W rejestrach tych nie będzie
ilorazu, ale
reszta z dzielenia!Dzięki temu mamy pewność, że wynik zawsze się zmieści w rejestrze 4-bajtowym. Pozostaje jeszcze problem
"jakąś liczbę". Jaką? Liczba ta powinna być 33 bitowa, z tym że na 1 i ostatnim bicie powinna być jedynka. Przy okazji. Proszę zwrócić uwagę na to, że CRC-N i CRC-O to rejestry
32 bitowe i że
33=32+1. A jej wartość? Jest wiele liczb spełniający wcześniej wymienione warunki. np.
4 614 984 567 (ponad 4 miliardy). Tak sobie strzeliłem. Ważne jest tylko, że nadajnik i odbiornik znają tą liczbę i w trakcie przesyłania kolejnego bitu stopniowo uaktualniana jest wartość w CRC-N i CRC-O. Podobnie, jak w rozdziale 3, były aktualizowane rejestry
RIN i
RS Na końcu przesyłania informacji właściwej, w CRC-N i CRC-O jest już ta reszta z dzielenia.
Oczywiście pod warunkiem że nie było zakłóceń na łączach! Sama wartość ilorazu jest nieważna. W drugim etapie porównywane są te wartości. Gdy były jednakowe to na końcu transmisji w CRC-0
powinny być same zera (oprócz niebieskiej komórki). Napisałem
powinny, a nie
będą. Metoda ta nie jest w 100% pewna. Może być tak, że zakłócenie na łączach, zmieni wartość przesyłanej 128 bajtowej liczby a obydwie reszty w CRC-N i CRC-O będą takie same. Dlatego, że np reszta z 39:6 to 3, i reszta z 21:6 też 3. Dwie różne liczby dają taką samą resztę. Ale musiałby to być naprawdę supertotolotek, żeby "zakłócona" liczba dała taką samą resztę jak '"niezakłócona". Zwłaszcza że dzielimy
bardzo, bardzo i jeszcze raz bardzo dużą liczbę (1024 bitową), przez tylko
bardzo dużą liczbę 33 bitową.
UwagaPrzesyłanie informacji następuje i obliczanie reszty w w CRC-N i CRC-O następują "bit po bicie". Tak też należy analizować rys. 3 i 4.
 Rys. 3 Nadajnik i odbiornik w czasie nadawania informacji właściwej (ETAP 1)
Rys. 3 Nadajnik i odbiornik w czasie nadawania informacji właściwej (ETAP 1)Przełącznik w położeniu
górnymKażdy takt (nie pokazany impuls zegarowy) "przepycha" 1 bit z
RN nadajnika do
RO odbiornika.
Jednocześnie każdy takt uaktualnia (oblicza) resztę z dzielenia w rejestrach CRC-N i CRC-O. Jeżeli nie występują błędy na kabelku między nadajnikiem i odbiornikiem, to CRC-N i CRC-O mają w każdym stanie takie same wartości.
 Rys. 4 Nadajnik i odbiornik w czasie nadawania informacji nadmiarowej (ETAP 2)
Rys. 4 Nadajnik i odbiornik w czasie nadawania informacji nadmiarowej (ETAP 2)Przełącznik w położeniu
dolnymW
RO jest już odebrana cała wiadomość z
RN. Ze względu na stan przełącznika w Odbiorniku,
RO nie będzie się już zmieniało.
Każdy takt (nie pokazany impuls zegarowy) "przepycha" 1 bit z
CRC-N nadajnika do
CRC-O odbiornika.
Gdy na początku etapu 2 wartości CRC-N i CRC-O były takie same
(transmisja bezbłędna) to na końcu etapu 2, 4 bajty CRC-O będą wyzerowane. Komórka niebieska w CRC-O (bitowa, dlatego mniejsza od 4 bajtowych), pełni funkcję przy porównywaniu liczb w CRC-N i CRC-O. Tak jak niebieska komórka w rozdziale 3.
Uwaga! Uwaga!W powyższym opisie używałem pojęcie
dzielenia. W rzeczywistości do obliczeń używa się działania
podobnego do prawdziwego dzielenia. Takie sobie
pseudodzielenie. Też daje coś podobnego do reszty. Za to
pseudodzielenie jest dużo szybsze niż
prawdziwe. Jest to bardzo ważne, gdyż zależy nam na tym, żeby wykrywanie błędów nie zwalniało transmisji.
Rozdz. 5 - JAK DZIAŁA PSEUDODZIELENIE?Dalej przeważnie będę pisał o pseudodzieleniu, a także pseudo... dodawaniu, odejmowaniu i mnożeniu. Dlatego dla wygody używajmy nazw bez pseudo, chociaż wiemy o co chodzi. Jeżeli będę się powoływał na "prawdziwe" działania, to wyraźnie zaznaczę.
Na początku napisałem, że wystarczy minimum teorii. Ale bez przesady. Zakładam, że wiesz jak podzielić pisemnie np. "23538:134". Znali to już Babilończycy. I co jest najciekawsze. Problem tak trywialny jak dzielenie, wrócił stosunkowo niedawno, około 50 lat temu do współczesnej matematyki. Zapotrzebowanie zgłosiła wtedy nowa dziedzina wiedzy - informatyka. Mianowicie jako sposób wykrywania błędów przy przesyłaniu danych - patrz rozdział 4. Zauważ, że gdybyśmy zastosowali prawdziwe dzielenie, nawet w wersji binarnej, to przy obliczaniu kolejnych reszt musimy korzystać z tzw. "przeniesień". Wicie, rozumicie. A gdyby wykombinować takie "dzielenie", w którym nie trzeba używać "przeniesień"? Działanie prostsze, i mniej korzystania z pamięci. Zawsze wtedy uaktualnianie CRC-N i CRC-O będzie szybsze i elektronika prostsza.
Później okaże się, że zamiast odejmować liczby przy obliczaniu kolejnej reszty, wystarczy je tylko
xor-ować. Dlatego warto dokładnie zapoznać się z
XOR-em.
Jak działa funkcja logiczna
XOR?
 Rys.5 Bramka XOR przy wszystkich kombinacjach wejść
Rys.5 Bramka XOR przy wszystkich kombinacjach wejść.
XOR można byłoby nazwać bardziej swojsko
"PORÓWNYWACZ". "0" na wyjściu oznacza, że 2 wejścia są takie same, "1" że różne.
Inne podejście do
XOR-a. Jest to układ o jednym wejściu, na które wchodzi informacja zero-jedynkowa. Drugie wejście S pełni funkcję sterującą. Gdy S=0 to przepuszcza bity bez zmian(wzmacniacz o wzmocnieniu=1), gdy S=1 to neguje je. Taki sobie sterowany wzmacniacz/negator
 Rys.6 XOR jako sterowany wzmacniacz/negator
Rys.6 XOR jako sterowany wzmacniacz/negator.
Jeszcze jedna interpretacja
XOR-a
 Rys.7 XOR jako "Dodawacz bez przeniesień"
Rys.7 XOR jako "Dodawacz bez przeniesień"Chyba nie wymaga komentarza. Proponuję też sprawdzenie, jak działa
XOR jako "Odejmowacz bez pożyczek". Okaże się że dodawanie i odejmowanie przy pomocy
XOR-owania, daje takie sam rezultat.Ja ciągle o
XOR-ach! Ale naprawdę warto. Później okaże się, że wykrywanie błędów to tylko przesuwanie rejestrów i ich
XOR-owanie.
Zobaczmy jak wyglądałoby dodawanie liczb dziesiętnych bez przeniesień Rys.8 Dodawanie liczb dziesiętnych bez przeniesieńAnalogicznie dodawanie, odejmowanie i mnożenie liczb binarnych bez przeniesień/pożyczek
Rys.8 Dodawanie liczb dziesiętnych bez przeniesieńAnalogicznie dodawanie, odejmowanie i mnożenie liczb binarnych bez przeniesień/pożyczek Rys.9 Dodawanie, odejmowanie i mnożenie liczb binarnych bez przeniesień/pożyczek
Rys.9 Dodawanie, odejmowanie i mnożenie liczb binarnych bez przeniesień/pożyczekOdejmowanie daje ten sam wynik co dodawanie. Gdyby ktoś miał problemy z mnożeniem, to proponuję wykonać pisemne mnożenie np. 12x17 najpierw "zwykłe"--> wynik 204 a potem bez przeniesień --> wynik 194
Umiemy już dodawać, odejmować i mnożyć po XOR-owsku. Pozostało na jeszcze dzielenie  Rys.10 Przykład dzielenia bez reszty
Rys.10 Przykład dzielenia bez resztyW szkole podstawowej naukę dzielenia pisemnego zaczynaliśmy od dzielenia bez reszty, np
48:3. Tu postąpimy podobnie. Na rysunku najpierw pomnożyliśmy pisemnie
xor-owo
1010x1101=1110010. Następnie wykonamy działanie odwrotne, czyli pisemnie podzielimy
1110010 przez
1101. I tak
1110 "mieści" się
1 raz w
1101 to piszemy nad kreską pierwsze
1. Potem od
1110odejmujemy
1101 jako
1x1101 - jak w zwykłym dzieleniu. Gdyby częściowa dzielna nie "mieściła" się,to piszemy nad kreską
0 i odejmujemy
0000 jako
0x1101. W ten sposób otrzymujemy kolejne reszty, aż do ostatniej
000. Ostatnie
000 oznacza, że udało podzielić się bez reszty, a nad główną kreską mamy iloraz.
Uwaga Częściowa dzielna "mieściłaby się" w
1101 także, gdyby była
1000.Dlaczego? Bo takie są dziwne zasady arytmetyki
xor-owej. Nie "mieściłaby" się dopiero, gdyby była np 0111 lub mniejsza, co już jest oczywiste. Męczy
1000>=1101? Trudno, takie jest życie. Wynika to chyba z tego, że
xor-owe dodawanie i odejmowanie, daje ten sam wynik. Patrz rys. 9.
Zaatakujmy teraz dzielenie z resztąPodejście pierwsze 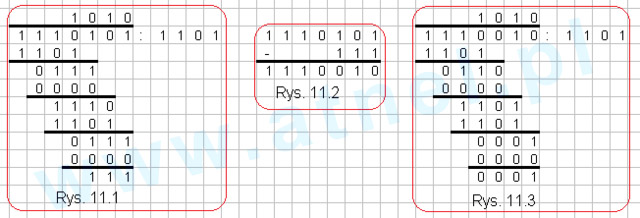 Rys. 11 Podejście pierwsze
Rys. 11 Podejście pierwsze Wiadomo, że jak weźmiemy 2 dowolne liczby całkowite to najprawdopodobniej po podzieleniu pozostanie jakaś reszta.
Wykonajmy więc działanie np.
1110101 : 1101. Od razu załóżmy, że nie interesuje nas coś, co możemy nazwać ilorazem-czyli liczba nad główną kreską. W transmisji też nie jest ważny iloraz, tylko
reszta. Rys. 11.1 pokazuje jak otrzymaliśmy resztę
111. Zaczynamy kombinować. W zwykłym dzieleniu jest np. 38:5 = 7 reszta 3, to wiadomo że
38-3=35 dzieli się bez reszty przez 5. Nie chcę się chwalić, sam na to wpadłem. Analogicznie od
1110101 odejmijmy resztę z rys. 11.1 czyli
111. Działanie to przedstawione jest na rys. 11.2 i daje wynik
1110010. Jest to odpowiednik, wcześniej wymienionej liczby
35. Oczekujemy więc, że po podzieleniu
1110010 przez
1011 otrzymamy resztę zerową. Działanie to przedstawia rys. 11.3. I co? Resztą jest
001, a nie
000.
Wniosek Pierwsze podejście się nie udało. Nie idź tą drogą!
Podejście drugie  Rys. 12 Podejście drugie
Rys. 12 Podejście drugie Ok. 50 lat temu, mądrzy ludzie wpadli na coś takiego.
Dzielnik ma n bitów.
1. Do ostatnich bitów dzielnej dołącz (n-1) zer. Nazwijmy to zmodyfikowaną dzielną.
2. Metodą pierwszego podejścia wykonaj dzielenie zmodyfikowanej dzielnej.
3. Na końcu otrzymasz resztę
Przedstawione jest to na
rys. 12.1 Szukamy reszty dla
1101011:1011. Dodajemy 3 zera (bo dzielnik 4-bitowy!). Czyli nowe podejście dla znalezienia reszty z
1101011:1011, to tak jakby to było pierwsze podejście dla
1101011000:1011! Otrzymaną resztą jest
110. Pamiętajmy, że jest to reszta dla
1101011:1011 a nie dla
1101011000:1011! 3 zera pełnią tylko funkcję pomocniczą.
Sprawdźmy, czy jest to rzeczywiście reszta.Na
rys. 12.2 odjęliśmy od zmodyfikowanej dzielnej resztę
1101011000 - 110 =1101011110 . Okazuje się, że jest to dzielna
1101011 z dodanymi 3 bitami reszty
110.
To teraz poznaną metodą obliczmy resztę z liczby
1101011 z dodanymi 3 bitami reszty
110. Czyli z liczby
1101011110. Patrz
rys. 12.3 Spodziewamy się reszty
000. Oczywiście, znowu musimy dodać 3 zera itd. Otrzymana reszta to
000. Zwycięstwo! Jeszcze jedno. Zauważ ze resztę
000 widać na końcu algorytmu, oraz wcześniej. Pokazują to strzałki przy
*Uwaga. Rzeczywiście, gdy dzielimy liczbę, która z założenia (jak na rys. 12.3) dzieli się bez reszty, to zerowa reszta
000 zawsze pojawi się wcześniej. Wykorzystamy tę właściwość w rozdziale 9 na rys. 14.3 gdzie sprawdzamy czy dana liczba dzieli się bez reszty przez dzielnik. Wtedy zamiast dołączać do dzielnej
same zera, dołączymy wcześniej obliczoną
resztę.
NAJWAŻNIEJSZY WNIOSEKDołączając bity reszty do dzielnej otrzymamy liczbę podzielną (bez reszty!) przez dzielnik.Przykład:
Dzielna
1101011110101Dzielnik
10111Reszta
1000Tzn że liczba
11010111101011000 dzieli się bez reszty przez 10111
Gdyby ta zasada obowiązywała w naszej "ludzkiej" arytmetyce to powstałoby takie dziwadło:
Przykład:
Dzielna
39Dzielnik
7Reszta
4Tzn że liczba
394 dzieli się bez reszty przez 7. ( a nie 35=39-4)
Rozdz.6 Kalkulator obliczania reszty CRC onlinePrzy okazji. To co nazywaliśmy
resztą, można nazwać bardziej dostojnie
reszta CRC.
Omówione wcześniej obliczanie reszty wymaga tylko małpiej zręczności. Nie mniej warto, chociaż raz w życiu zrobić to ręcznie. Chyba każdy student czegoś co ma związek z informatyką, przez to przeszedł. Jak już to umiesz, to nie warto się męczyć, tylko skorzystać z kalkulatora CRC. Tu polecam stronę
http://www.leischner.inf.fh-bonn-rhein- ... at/crc.htm. Jest to łatwy kalkulatorek bez niepotrzebnych wodotrysków, stworzony w Hochshule Bonn-Rhein-Sieg. Wystarczy wpisać dzielną, dzielnik, a kalkulator sam doda zera i bzziuu... Myślę że Rys. 13 jest wystarczającą instrukcją.Proponuję sprawdzić wcześniej podane przykłady. Zwłaszcza, że jak do do ostatnich bitów dzielnej dopiszemy resztę
(którą oczywiście wcześniej obliczyliśmy kalkulatorem!) i ponownie obliczymy resztę,
to będzie zerowa!. W podanym na Rys. 13 przykładzie, kalkulator liczy to samo, co my ręcznie na rys. 12.1.
 Rys. 13 kalkulator reszty (CRC)Rozdz. 7 Zamieńmy algorytm obliczania reszty CRC w algorytm używający rejestrów przesuwnychUwagi ogólne o dwóch szkołach rozgryzania algorytmówSzkoła nr 1 - naukowa, mądra, elegancka, ogólna - trudna do zrozumienia
Rys. 13 kalkulator reszty (CRC)Rozdz. 7 Zamieńmy algorytm obliczania reszty CRC w algorytm używający rejestrów przesuwnychUwagi ogólne o dwóch szkołach rozgryzania algorytmówSzkoła nr 1 - naukowa, mądra, elegancka, ogólna - trudna do zrozumieniaStosowana w rozprawach, pracach magisterskich czy doktorskich. Inaczej nie wypada.
Przykład. Chcemy wytłumaczyć jak dzielić 2 liczby dziesiętne.
Zaczyna się tak. Załóżmy że dzielna ma n cyfr i dzielnik ma m cyfr. Nad dzielną narysujmy kreskę. Pod najbardziej znaczącą dzielną napiszmy dzielnik tak że najbardziej znacząca cyfra dzielnika ... itd itd. Metoda ta ma same zalety, w tym że dotyczy wszystkich n-cyfrowych
dzieln i m-cyfrowych
dzielników. Ma tylko jedną wadę. Jest mało
intuicyjna.
Szkoła nr 2 - "nienaukowa", "nieelegancka", nieogólna- za to łatwa do zrozumieniaWykorzystujemy konkretny przykład. Np
126588:137 Z tą metodą zetknąłeś się chyba w 4 klasie szkoły podstawowej. Trochę wstyd ją używać, ale ma jedną podstawową zaletę. Jest
intuicyjna. I chociaż poznałeś tylko jeden przykład, to nie znaczy że do końca życia będziesz umiał dzielić tylko
126588 przez
137. Umiesz przecież dzielić wszystkie liczby! Czyli też jest
ogólna. Chociaż dla rasowego matematyka nauczyłeś się dzielić tylko te 2 w/w liczby.
Do wyjaśnienia wykrywania błędów transmisji przy pomocy
CRC zastosuję
szkołę nr 2- Tzn bardzo dokładnie rozpatrzę jak działa wykrywanie błędów gdy
dzielną (wysyłaną informacją) jest liczba
100011, dzielnikiem
1011 a obliczoną resztą będzie
111. Reszta będzie obliczana w pewnego rodzaju rejestrze przesuwnym, którego strukturę spróbujemy wykryć.
Następnie tę strukturę uogólnimy na dowolny dzielnik. Właśnie w tym zdaniu tkwi "nieścisłość" tej metody. No cóż, zastosowaliśmy może niezbyt etyczną zasadę. Nieważne są
środki prowadzące do celu, ważny jest
cel. Najważniejsze że będziesz czuł jak to działa.
 Rys. 14.1 "Rejestrowa" wersja algorytmuOpis ogólny
Rys. 14.1 "Rejestrowa" wersja algorytmuOpis ogólnyOmawiany algorytm będzie "rejestrową" wersją algorytmu klasycznego (np z rys. 12.1 , 13). Dalej to już tylko krok do zaprojektowania odpowiedniej elektroniki. Do
rejestru CRC wprowadzana jest bit po bicie dzielna np.
100011000 z 3 dodatkowymi zerami. Przy każdym wprowadzeniu bitu, rejestr
CRC jest w prosty sposób uaktualniany. Co prawda, już nie tak prosto jak zwykłe przesunięcie, ale jeszcze w sposób możliwy do łyknięcia. Na zakończenie
rejestr CRC będzie zawierał resztę z dzielenia. Proszę zwrócić uwagę na to,
że takie "nic", jak to 3-bitowe CRC, oblicza resztę z dzielenia, nawet z większej dzielnej np. o długości 10 tys. bitów!!!Stan początkowy algorytmu (rys. 14.1)
rejestr Dzielna +3 zera - rejestr przesuwny którego stanem początkowym jest
100011000 (
100011 to komunikat przeznaczony do wysłania)
rejestr CRC - rejestr 3-bitowy którego stanem początkowym jest
000rejestr Dzielnik - Stała pamięć
ROM zawierająca dzielnik
1011. Jak to w
ROM-ie, zawartość się nie zmienia.
Sercem układu jest
CRC. Jest on wyższą szkołą jazdy rejestrów przesuwnych. W zwykłym rejestrze nowy stan, to po prostu przesunięte w lewo bity. W
CRC bity mogą być tylko przesunięte. Ale mogą być też po przesunięciu
xor-owane z trzema najmłodszymi bitami
Dzielnika (tu
011). Czyli
xor-owane będzie "niebieskie z zielonym". Przy każdym przesunięciu
Dzielna +3 zera jest skracana o 1 bit. Algorytm się skończy, gdy
Dzielna +3 zera zniknie całkowicie. Wtedy
CRC będzie zawierał
resztę z dzielenia.
 Rys. 14.2. Jak działa "rejestrowy" algorytm obliczania reszty CRC
Rys. 14.2. Jak działa "rejestrowy" algorytm obliczania reszty CRC Każdy (niepokazany na rysunku) impuls zegarowy wprowadza aktualnie najstarszy bit z
Dzielna + 3 zera do
CRC. Za każdym razem
Dzielna + 3 zera skraca się o jeden bit. Pokazano "fotografie" rejestrów w każdym z 9 stanów.
Stan 0 to stan początkowy (jak na rys. 14.1) a
stan 9 to końcowy. W tym stanie w
CRC jest już ostatecznie obliczona reszta z dzielenia - tu
111.
Uwaga Algorytm obliczania reszty CRC będzie wymagał
xor-owania:
- 3 najmłodszych najmłodszych bitów ("niebieskich")
Dzielnika -->
011- z 3 bitami ("zielonymi")
CRC Algorytm jest bardzo prosty1 - Jeżeli najstarszy bit
CRC = 0 , to w następnym stanie tylko przesuń
CRC i Dzielna + 3 zera o 1 bit w lewo.
2 - Jeżeli najstarszy bit
CRC = 1 to w następnym stanie :
......Przesuń
CRC i Dzielna+3 zera o 1 bit w lewo.
......Potem
xor-uj 3 najmłodsze bity
Dzielnika (tu
011) z bitami
CRCPrzy każdym stanie na rys. 14.2 jest polecenie wynikające z w/w algorytmu. Gdy
najstarszy bit
CRC = 0 to tylko przesuń w lewo, a gdy
1 to itd... Efekt tego polecenia jest oczywiście widoczny w następnym stanie.
Przykład:W stanie 3 CRC=100 i
Dzielna + 3 zera = 011000 W stanie 4 - po przesunięciu
CRC=000 (ten stan nie jest pokazany na rysunku)
- po xor-owaniu
000 z
011 CRC=011Na podstawie rys. 14.2 można, już zrealizować układ obliczający resztę z dzielenia!
Bezpośrednio na rejestrach i xor-ach! Rozdział
8 pokaże, że można to zrobić jeszcze prościej.
 Rys. 14.3. Sprawdzenie czy komunikat 1000011 + reszta 111, da nam resztę 000?
Rys. 14.3. Sprawdzenie czy komunikat 1000011 + reszta 111, da nam resztę 000?Na rys. 14.2 do komunikatu w stanie 0 dołączyliśmy 000. W ten sposób w stanie 9 otrzymaliśmy
resztę=111 z dzielenia
100011:1011. A co by było, gdyby zamiast
000 wstawić resztę
111? Okaże się, że obliczona reszta to
000. Jest to zgodne z
xor-ową teorią dzielenia. W rozdz. 6 stwierdziliśmy
"Dołączając bity reszty do dzielnej, otrzymamy liczbę podzielną (bez reszty!) przez dzielnik".Ciąg dalszy w
Jak CRC wykrywa błędy transmisji? część.2 LINK  Kanał - ATNEL tech-forum
Kanał - ATNEL tech-forum Wszystkie działy
Wszystkie działy Najnowsze wątki
Najnowsze wątki




